
数据结构与算法
1.数据结构
1.1数据结构是什么
数据结构(data structure)是组织和存储数据的方式,涵盖数据内容、数据之间关系和数据操作方法,它具有以下设计目标。
空间占用尽量少,以节省计算机内存。
数据操作尽可能快速,涵盖数据访问、添加、删除、更新等。
提供简洁的数据表示和逻辑信息,以便算法高效运行。 数据结构设计是一个充满权衡的过程。如果想在某方面取得提升,往往需要在另一方面作出妥协。下面举两个例子。
链表相较于数组,在数据添加和删除操作上更加便捷,但牺牲了数据访问速度。
图相较于链表,提供了更丰富的逻辑信息,但需要占用更大的内存空间。
1.2数据结构的分类
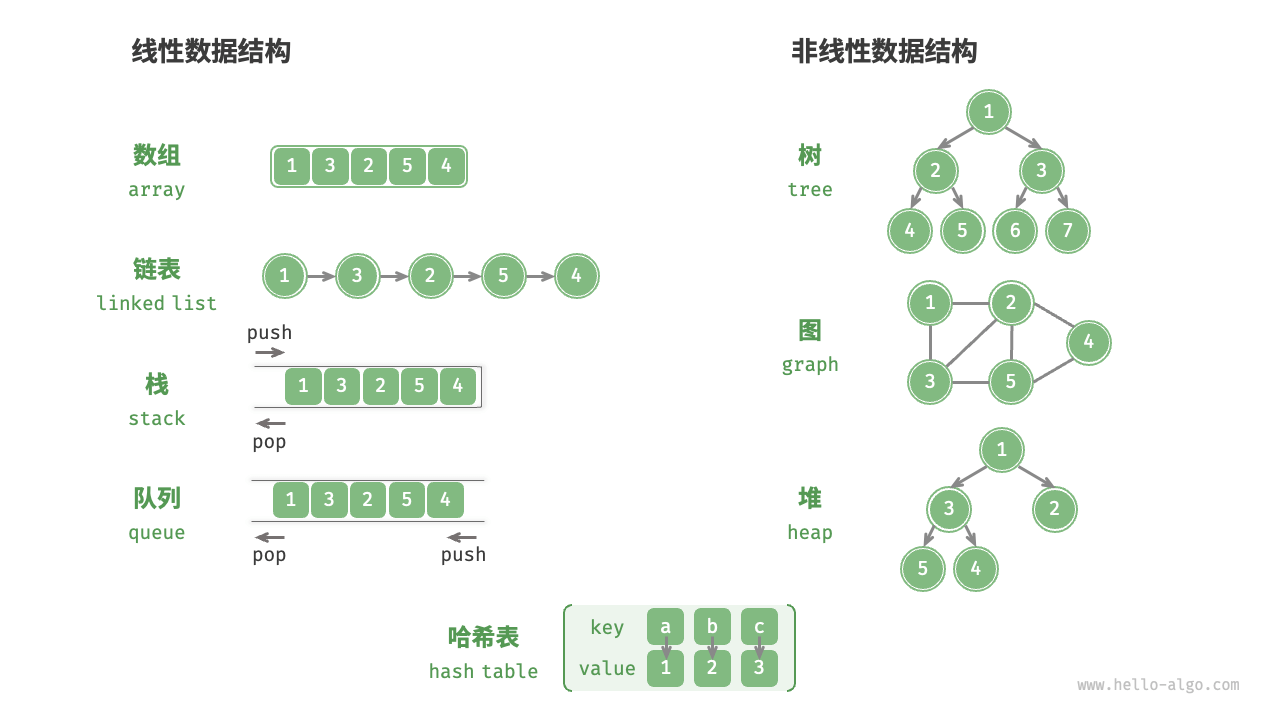
1️⃣ 逻辑结构的分类
- 线性结构:数组,链表,栈,队列,哈希表
- 非线性结构:树,堆,图
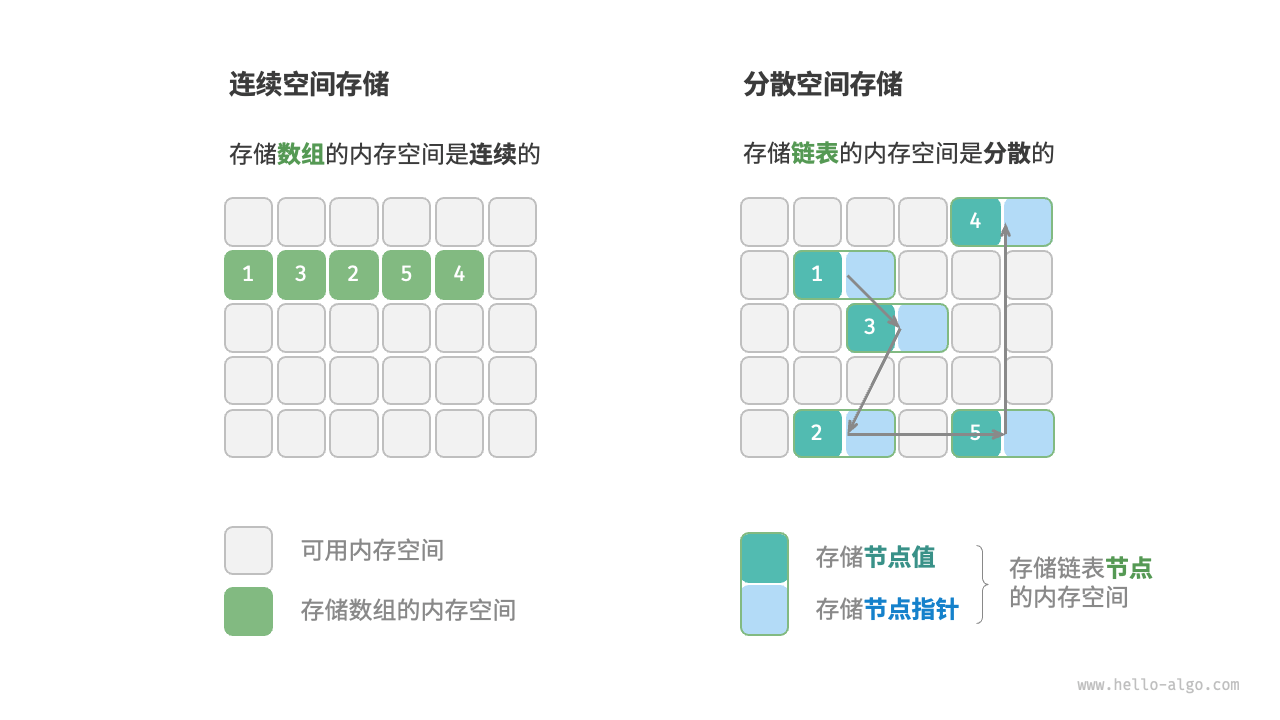
2️⃣ 物理结构的分类
- 顺序结构:划分连续内存空间(元素顺序访问)
- 链式结构:使用分散内存空间(内存寻址访问)
1.3数字编码格式
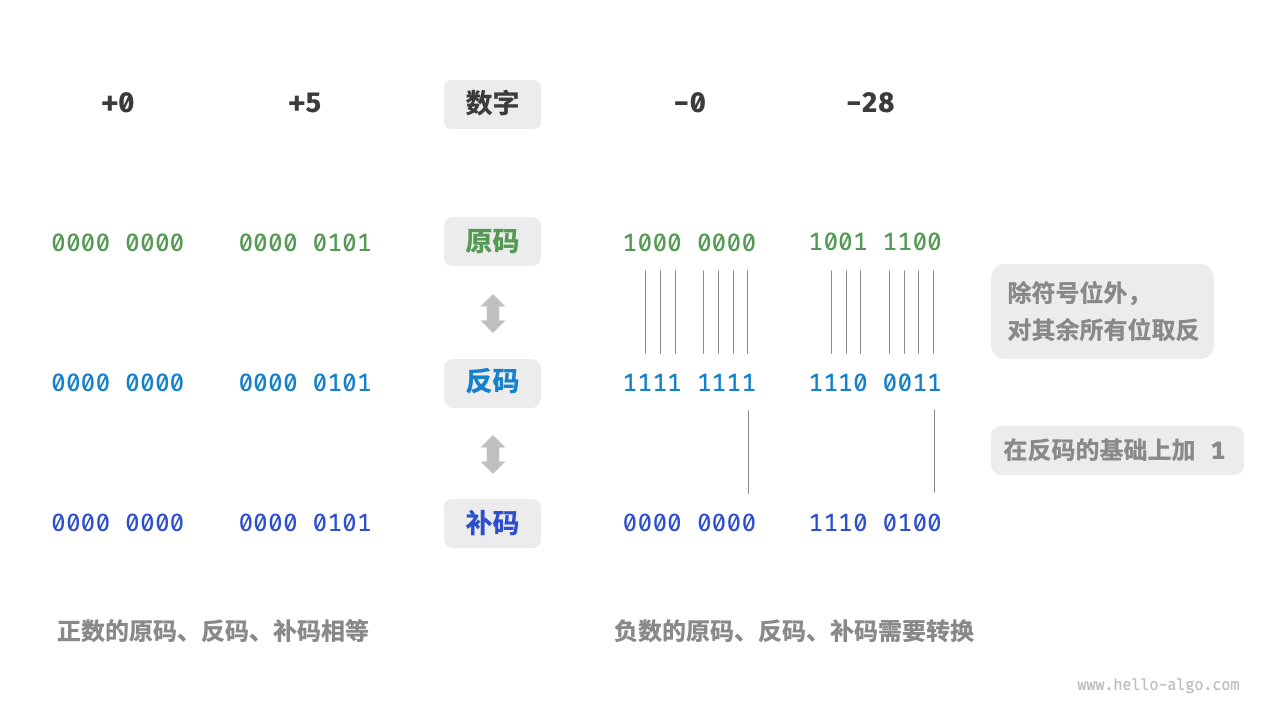
- 原码:数字的二进制表示的最高位视为符号位,其中 表示
0正数,1表示负数,其余位表示数字的值。 - 补码:正数的补码与其原码相同,负数的补码是在其反码的基础上加
1。 - 反码:正数的反码与其原码相同,负数的反码是对其原码除符号位外的所有位取反。
- 浮点数编码:
IEEE 754 是一种广泛使用的浮点数编码格式标准,它定义了浮点数的编码格式、运算规则和异常处理机制。IEEE 754 浮点数编码格式包括以下几种:
- 单精度浮点数(Single Precision)
单精度浮点数使用 32 位二进制代码来表示实数,包括:
- 符号位(Sign bit):1 位,表示数的符号(正或负)
- 指数位(Exponent bits):8 位,表示指数的值
- 尾数位(Mantissa bits):23 位,表示尾数的值
- 双精度浮点数(Double Precision)
双精度浮点数使用 64 位二进制代码来表示实数,包括:
- 符号位(Sign bit):1 位,表示数的符号(正或负)
- 指数位(Exponent bits):11 位,表示指数的值
- 尾数位(Mantissa bits):52 位,表示尾数的值
- 扩展精度浮点数(Extended Precision)
扩展精度浮点数使用 80 位二进制代码来表示实数,包括:
- 符号位(Sign bit):1 位,表示数的符号(正或负)
- 指数位(Exponent bits):15 位,表示指数的值
- 尾数位(Mantissa bits):64 位,表示尾数的值
2.算法
2.1算法是什么
算法是解决特定问题的一系列步骤或规则。它可以被看作是一个清晰的指令集合,用于完成特定的任务或计算。算法通常涉及以下几个方面:
- 输入:算法接收某些数据或参数作为输入。
- 处理:算法通过一系列步骤对输入数据进行处理。
- 输出:算法产生结果或输出,完成任务。
算法可以用来解决各种问题,如排序、搜索、计算、图像处理等。它们可以用不同的编程语言实现,并且在计算机科学中,算法是编程和数据处理的核心。
2.2算法效率的评估
在算法设计中,我们先后追求以下两个层面的目标。
- **找到问题解法:**算法需要在规定的输入范围内可靠地求得问题的正确解。
- **寻求最优解法:**同一个问题可能存在多种解法,我们希望找到尽可能高效的算法。 也就是说,在能够解决问题的前提下,算法效率已成为衡量算法优劣的主要评价指标,它包括以下两个维度。
- 时间效率:算法运行时间的长短。
- 空间效率:算法占用内存空间的大小。 简而言之,我们的目标是设计“既快又省”的数据结构与算法。而有效地评估算法效率至关重要,因为只有这样,我们才能将各种算法进行对比,进而指导算法设计与优化过程。
效率评估方法主要分为两种:实际测试、理论估算。
2.3算法中的迭代与递归
在算法中,重复执行某个任务是很常见的,它与复杂度分析息息相关。因此,在介绍时间复杂度和空间复杂度之前,我们先来了解如何在程序中实现重复执行任务,即两种基本的程序控制结构:迭代、递归。
2.3.1迭代
迭代(iteration)是一种重复执行某个任务的控制结构。在迭代中,程序会在满足一定的条件下重复执行某段代码,直到这个条件不再满足。
- for循环
- while循环
2.3.2递归
递归(recursion)是一种算法策略,通过函数调用自身来解决问题。它主要包含两个阶段。
递:程序不断深入地调用自身,通常传入更小或更简化的参数,直到达到“终止条件”。
归:触发“终止条件”后,程序从最深层的递归函数开始逐层返回,汇聚每一层的结果。 而从实现的角度看,递归代码主要包含三个要素。
终止条件:用于决定什么时候由“递”转“归”。
递归调用:对应“递”,函数调用自身,通常输入更小或更简化的参数。
返回结果:对应“归”,将当前递归层级的结果返回至上一层。
2.3.3选择迭代还是递归
- 迭代:适用于大多数简单的循环任务,通常更高效,且没有栈溢出风险。
- 递归:适用于问题可以自然地分解为更小的相似问题的情况,如树结构遍历、图遍历、数学归纳法问题等。
2.4时间复杂度
算法的时间复杂度是衡量算法执行所需时间的指标,它反映了算法在处理输入数据时,随着数据规模的增大,执行时间的增长速度。时间复杂度通常用大O符号表示(O-notation),常见的时间复杂度有:
O(1):常数时间复杂度,不论输入数据规模多大,算法的执行时间都是固定的。例如,访问数组的某个元素。
O(log n):对数时间复杂度,通常出现在二分查找等算法中,数据规模增加,时间复杂度的增长速度较慢。例如,二分查找在有序数组中的查找。
O(n):线性时间复杂度,算法的执行时间与输入数据规模成正比。例如,遍历一个数组。
O(n log n):线性对数时间复杂度,常见于许多高效的排序算法,如快速排序和归并排序。
O(n²):平方时间复杂度,常见于一些简单的排序算法,如冒泡排序和选择排序,以及双层循环的情况。
O(2^n):指数时间复杂度,通常出现在一些递归算法中,例如求解斐波那契数列的朴素递归解法。
O(n!):阶乘时间复杂度,通常出现在一些组合问题中,例如旅行商问题的暴力解法。
理解时间复杂度有助于评估算法在处理大规模数据时的表现,并选择最适合的算法和优化策略。
2.5空间复杂度
空间复杂度是衡量算法在执行过程中所占用的存储空间的指标。它反映了随着输入数据规模的增大,算法所需存储空间的增长速度。空间复杂度同样使用大O符号表示,常见的空间复杂度包括:
O(1):常数空间复杂度,算法所需的空间不随输入数据规模的增大而增加。例如,简单的变量赋值操作或对数组元素的直接访问。
O(n):线性空间复杂度,算法所需的空间与输入数据规模成正比。例如,将输入数据复制到另一个数组或列表中。
O(log n):对数空间复杂度,通常出现在递归算法中,递归深度为log n时,所需的额外空间也是log n。
O(n log n):线性对数空间复杂度,通常出现在一些需要额外临时存储的递归或分治算法中。
O(n²):平方空间复杂度,算法所需的空间与输入数据规模的平方成正比。例如,在矩阵运算中,需要存储一个n x n的矩阵。
空间复杂度的考虑因素
- 辅助空间(Auxiliary Space):除了输入数据之外,算法执行过程中所需的额外空间。例如,排序算法中的临时存储空间。
- 输入数据空间:算法处理输入数据时所占用的空间。
典型例子
- 递归调用:递归算法的空间复杂度通常与递归深度有关,因为每次递归调用都会占用栈空间。
- 动态规划:某些动态规划算法需要使用额外的数组来存储中间结果,其空间复杂度通常为O(n)或O(n²)。
理解空间复杂度有助于优化算法,尤其在处理大数据或内存受限的环境中,空间复杂度是选择合适算法的重要考虑因素之一。
