数学建模

Jianghu原创大约 5 分钟

知识点

001 数学建模竞赛介绍 7.29 A
002 线性规划和整数规划模型 7.30 A
003 非线性规划和多目标规范模型 7.31 A
004 常微分方程 8.1 B
005 差分方程 8.2 B
006 偏微分方程 8.3 C
007 Python 数学建模基础 8.4 D
008 插值方法 8.5 C
009 最短路问题、最小生成树问题 8.6 E
010 最大流与最小费用问题 8.7 E
011 背包问题、指派问题、旅行商问题 8.8 E
012 智能优化算法 8.9 F
013 Matlab 软件处理 1 8.10 G
014 Matlab 软件处理 2 8.11 G
015 数据处理方法（Python） 8.12 D
016 统计分析方法 8.13 H
017 回归模型与分析 8.14 H
018 聚类分析方法与判别分析 8.15 F
019 主成分分析方法（数据降维） 8.16 I
020 预测方法 8.17 J
021 SPSS 统计分析 8.18 A
022 几何模型 8.19 B
023 博弈模型 8.20 F
024 综合评价方法 8.21 J
025 数字图像处理 8.22 C
026 数学建模竞赛论文写作 8.23 A
027 数学建模竞赛(A 题)讲解 8.24 C
028 数学建模竞赛(B 题)讲解 8.25 J
029 数学建模竞赛(C 题)讲解 8.26 F
030 数学建模竞赛(D 题)讲解 8.27 A
031 数学建模竞赛(E 题)讲解 8.28 B
032 数学建模竞赛(F 题)讲解

中国研究生数学建模竞赛

网址：https://cpipc.acge.org.cn/
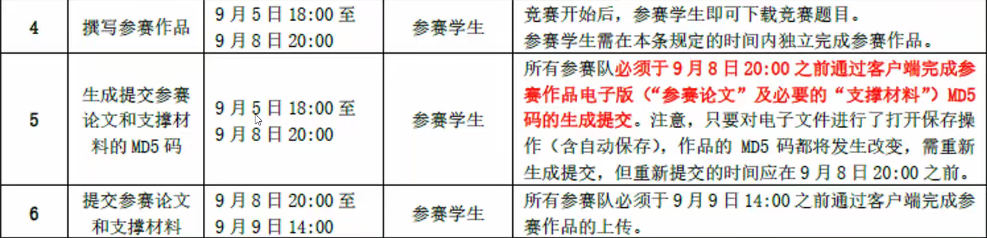
通知材料：竞赛规则：

数学建模

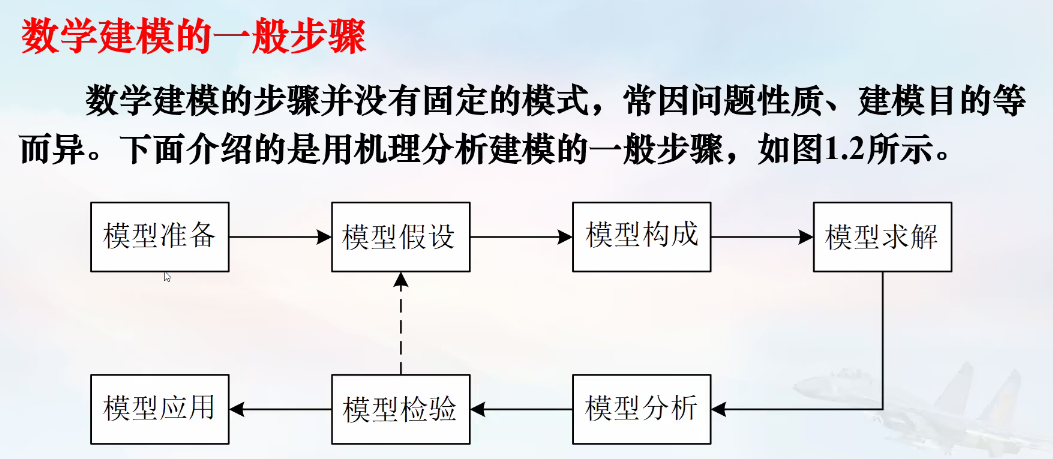
数学建模是将实际问题转化为数学问题，从而利用数学方法进行分析和解决的过程。以下是数学建模的基本步骤和常用方法：

数学建模的基本步骤

问题描述：明确问题的背景、目标和约束条件。
假设条件：简化和抽象问题，提出合理的假设。
建立模型：根据问题和假设，选择合适的数学方法，建立数学模型。
求解模型：利用数学工具和计算方法求解模型。
模型验证：将求解结果与实际情况进行比较，验证模型的合理性。
模型改进：根据验证结果，调整假设和模型，进行改进。
结果分析与解释：对模型结果进行分析，解释其实际意义，并提出建议。

常用的数学建模方法

优化模型：
- 线性规划：用于求解线性目标函数的最优化问题，常用工具有Simplex方法。
- 非线性规划：用于求解非线性目标函数的最优化问题，常用工具有Lagrange乘数法。
- 整数规划：求解变量为整数的优化问题，常用于组合优化问题。
- 动态规划：用于多阶段决策问题，常用来解决路径优化、资源分配等问题。
统计模型：
- 回归分析：建立变量之间的关系模型，常用于预测和因果分析。
- 时间序列分析：分析时间序列数据的规律，常用于经济、金融领域的预测。
- 假设检验：用于验证数据是否符合某种假设。
微分方程模型：
- 常微分方程：用于描述随时间变化的连续系统。
- 偏微分方程：用于描述空间和时间变化的连续系统。
仿真模型：
- 蒙特卡罗模拟：通过随机抽样和统计分析解决复杂问题。
- 离散事件模拟：模拟离散事件的发生过程，常用于排队论、生产系统等领域。
图论模型：
- 最短路径问题：求解图中两点之间的最短路径，常用算法有Dijkstra算法。
- 最大流问题：求解网络中从源点到汇点的最大流量，常用算法有Ford-Fulkerson算法。

数学建模软件和工具

MATLAB：强大的数值计算和建模工具，广泛应用于工程、科学等领域。
Python：具有丰富的科学计算库，如NumPy、SciPy、Pandas等，非常适合数据分析和建模。
R：专门用于统计分析和数据挖掘，拥有丰富的统计和图形工具。
GAMS：高级建模系统，特别适用于优化问题。
Excel：简单易用的表格工具，适合基础的数据处理和建模。

示例：简单的线性规划模型

假设有一个生产问题，生产两种产品，每种产品的利润分别为 $(P_1)$ 和 $(P_2)$ ，生产需要消耗资源，资源总量有限。设生产的数量分别为 $(x_1)$ 和 $(x_2)$ ，资源限制条件为 $(a_1x_1 + a_2x_2 \leq b)$ 。目标是最大化利润。

模型描述：

目标函数：最大化 (P_1 x_1 + P_2 x_2)
约束条件：(a_1 x_1 + a_2 x_2 \leq b) 和 (x_1 \geq 0), (x_2 \geq 0)

求解：

from scipy.optimize import linprog

c = [-P_1, -P_2]  # 目标函数系数（取负号因为scipy是最小化问题）
A = [[a_1, a_2]]  # 约束系数矩阵
b = [b]  # 约束条件

x_bounds = (0, None)
res = linprog(c, A_ub=A, b_ub=b, bounds=[x_bounds, x_bounds])

print(f"Optimal value: {-res.fun}")
print(f"Optimal solution: x1 = {res.x[0]}, x2 = {res.x[1]}")