跳至主要內容

插值与拟合

Jianghu原创大约 8 分钟数学建模数学建模

插值

插值是一种在已知数据点之间估算未知数据点的数学方法。它在数据分析、计算机图形学、信号处理、工程建模等多个领域有广泛应用。通过插值，我们可以构建一个连续的函数，这个函数在已知数据点处精确等于已知值，并且能够在这些点之间平滑地过渡。

插值方法

  1. 线性插值（Linear Interpolation）

    • 概念：在线性插值中，我们假设已知数据点之间的关系是线性的。每两个相邻的已知点之间用一条直线连接。
    • 公式：对于两个已知点 (x0,y0)(x_0, y_0) 和 (x1,y1)(x_1, y_1)，对于任意的 xx 值，插值结果 yy 可以表示为：

      y=y0+(y1−y0)x−x0x1−x0 y = y_0 + (y_1 - y_0) \frac{x - x_0}{x_1 - x_0}

  2. 多项式插值（Polynomial Interpolation）

    • 概念：多项式插值通过一个多项式函数来拟合所有已知点。常见的多项式插值方法包括拉格朗日插值和牛顿插值。
    • 拉格朗日插值公式：

      P(x)=∑i=0nyi∏0≤j≤nj≠ix−xjxi−xj P(x) = \sum_{i=0}^{n} y_i \prod_{\substack{0 \le j \le n \\ j \ne i}} \frac{x - x_j}{x_i - x_j}

    • 牛顿插值公式：基于差分商的递归公式，构建一个多项式。

  3. 样条插值（Spline Interpolation）

    • 概念：样条插值使用低阶多项式（通常是三次多项式）在每两个已知点之间进行插值，确保曲线的平滑性。
    • 自然三次样条：在每个区间内使用三次多项式，并且在区间连接处保证函数及其一阶和二阶导数的连续性。

  4. 其他插值方法

    • 最近邻插值（Nearest-Neighbor Interpolation）：每个未知点的值等于距离最近的已知点的值。
    • 双线性插值（Bilinear Interpolation）：二维数据的插值方法，通过在两个方向上分别进行线性插值来估算未知点的值。

Python中的插值实例

Python中可以使用SciPy库进行插值。以下是一些常见的插值方法的示例：

线性插值

import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt

# 已知数据点
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 1, 4, 9, 16, 25])

# 需要插值的点
x_new = np.linspace(0, 5, 50)

# 线性插值
f = interpolate.interp1d(x, y)

# 计算插值
y_new = f(x_new)

# 绘制结果
plt.plot(x, y, 'o', label='Known Points')
plt.plot(x_new, y_new, '-', label='Linear Interpolation')
plt.legend()
plt.show()

样条插值

import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt

# 已知数据点
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 1, 4, 9, 16, 25])

# 需要插值的点
x_new = np.linspace(0, 5, 50)

# 样条插值
tck = interpolate.splrep(x, y)
y_new = interpolate.splev(x_new, tck)

# 绘制结果
plt.plot(x, y, 'o', label='Known Points')
plt.plot(x_new, y_new, '-', label='Spline Interpolation')
plt.legend()
plt.show()

拉格朗日插值

import numpy as np
from scipy.interpolate import lagrange
import matplotlib.pyplot as plt

# 已知数据点
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 1, 4, 9, 16, 25])

# 拉格朗日插值
poly = lagrange(x, y)

# 需要插值的点
x_new = np.linspace(0, 5, 50)
y_new = poly(x_new)

# 绘制结果
plt.plot(x, y, 'o', label='Known Points')
plt.plot(x_new, y_new, '-', label='Lagrange Interpolation')
plt.legend()
plt.show()

拟合

拟合是一种通过数学模型逼近数据点的方法，旨在找到一个函数，使其尽可能地通过所有已知数据点或尽可能地逼近数据的总体趋势。拟合在统计学、数据分析、机器学习和工程建模中有广泛应用。拟合方法可以分为插值（通过所有数据点）和回归（逼近数据趋势，但不一定通过所有数据点）。

拟合方法

  1. 线性回归（Linear Regression）

    • 概念：线性回归假设因变量与自变量之间呈线性关系，通过最小化误差平方和来确定模型参数。
    • 公式：对于简单线性回归模型 y=a+bxy = a + bx，其中 aa 和 bb 是待定参数。

  2. 多项式拟合（Polynomial Fitting）

    • 概念：多项式拟合通过一个多项式函数来逼近数据点，可以是线性的、二次的、三次的等。
    • 公式：一般形式为 y=a0+a1x+a2x2+⋯+anxny = a_0 + a_1x + a_2x^2 + \cdots + a_nx^n，其中 a0,a1,…,ana_0, a_1, \ldots, a_n 是待定参数。

  3. 非线性拟合（Non-linear Fitting）

    • 概念：非线性拟合用于模型非线性关系的数据，模型形式和参数的确定通常需要迭代优化算法。
    • 例子：指数函数拟合 y=aebxy = a e^{bx} 或幂函数拟合 y=axby = ax^b。

  4. 最小二乘法（Least Squares Method）

    • 概念：最小二乘法是一种常见的拟合方法，通过最小化观测值与拟合函数之间的误差平方和来确定模型参数。
    • 应用：可以用于线性回归、多项式拟合等。

  5. 样条拟合（Spline Fitting）

    • 概念：样条拟合使用低阶多项式片段在各个数据点之间进行拟合，以确保曲线的光滑性。
    • 例子：三次样条拟合（Cubic Spline Fitting）。

Python中的拟合实例

Python中可以使用SciPy和NumPy库进行数据拟合。以下是一些常见的拟合方法的示例：

线性回归

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# 已知数据点
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 1, 4, 9, 16, 25])

# 线性回归
slope, intercept, r_value, p_value, std_err = stats.linregress(x, y)

# 拟合线
y_fit = intercept + slope * x

# 绘制结果
plt.plot(x, y, 'o', label='Known Points')
plt.plot(x, y_fit, '-', label='Linear Regression')
plt.legend()
plt.show()

多项式拟合

import numpy as np
import matplotlib.pyplot as plt

# 已知数据点
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 1, 4, 9, 16, 25])

# 多项式拟合（2次）
coeffs = np.polyfit(x, y, 2)
poly = np.poly1d(coeffs)

# 需要拟合的点
x_new = np.linspace(0, 5, 50)
y_new = poly(x_new)

# 绘制结果
plt.plot(x, y, 'o', label='Known Points')
plt.plot(x_new, y_new, '-', label='Polynomial Fitting (2nd Degree)')
plt.legend()
plt.show()

非线性拟合

import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt

# 已知数据点
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 1, 4, 9, 16, 25])

# 非线性函数定义
def func(x, a, b, c):
    return a * np.exp(b * x) + c

# 非线性拟合
popt, pcov = curve_fit(func, x, y)

# 需要拟合的点
x_new = np.linspace(0, 5, 50)
y_new = func(x_new, *popt)

# 绘制结果
plt.plot(x, y, 'o', label='Known Points')
plt.plot(x_new, y_new, '-', label='Non-linear Fitting')
plt.legend()
plt.show()

样条拟合

import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt

# 已知数据点
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 1, 4, 9, 16, 25])

# 样条拟合
tck = interpolate.splrep(x, y)
y_new = interpolate.splev(np.linspace(0, 5, 50), tck)

# 绘制结果
plt.plot(x, y, 'o', label='Known Points')
plt.plot(np.linspace(0, 5, 50), y_new, '-', label='Spline Fitting')
plt.legend()
plt.show()

插值和拟合的实例

Python 图像处理中的插值与拟合

图像处理中的插值与拟合广泛应用于图像放大、旋转、变形、图像恢复等操作。这里我们将展示一个如何在图像缩放过程中应用插值的例子，以及如何在音频信号处理中进行插值与拟合。

图像插值示例

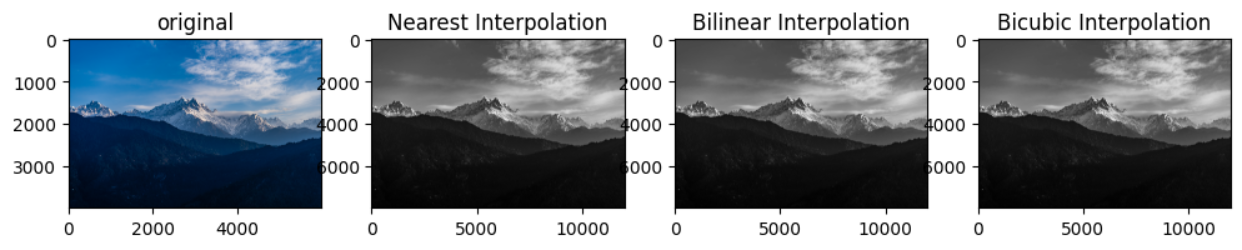
在图像处理中，常见的插值方法包括最近邻插值、双线性插值和双三次插值等。我们将使用OpenCV库来演示图像缩放中的插值方法。

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像
img = cv2.imread('input_image.jpg', cv2.IMREAD_GRAYSCALE)

# 获取图像尺寸
height, width = img.shape

# 设置缩放比例
scale_factor = 2

# 最近邻插值
nearest_img = cv2.resize(img, (width*scale_factor, height*scale_factor), interpolation=cv2.INTER_NEAREST)

# 双线性插值
bilinear_img = cv2.resize(img, (width*scale_factor, height*scale_factor), interpolation=cv2.INTER_LINEAR)

# 双三次插值
bicubic_img = cv2.resize(img, (width*scale_factor, height*scale_factor), interpolation=cv2.INTER_CUBIC)

# 绘制结果
plt.figure(figsize=(12, 4))

plt.subplot(1, 3, 1)
plt.title('Nearest Interpolation')
plt.imshow(nearest_img, cmap='gray')

plt.subplot(1, 3, 2)
plt.title('Bilinear Interpolation')
plt.imshow(bilinear_img, cmap='gray')

plt.subplot(1, 3, 3)
plt.title('Bicubic Interpolation')
plt.imshow(bicubic_img, cmap='gray')

plt.show()

output

请注意，在运行此代码前需要安装OpenCV库，并准备一个名为 input_image.jpg 的图像文件。

音频处理中的插值与拟合

音频处理中的插值与拟合常用于信号重采样、降噪、音高变换等。这里我们将演示如何使用SciPy库对音频信号进行插值和多项式拟合。

import numpy as np
import scipy.signal
import scipy.io.wavfile as wav
import matplotlib.pyplot as plt

# 读取音频文件
sample_rate, data = wav.read('input_audio.wav')

# 生成时间轴
t = np.linspace(0, len(data) / sample_rate, num=len(data))

# 缩短音频信号（下采样）
factor = 2
shortened_data = data[::factor]
shortened_t = t[::factor]

# 线性插值重建音频信号
linear_interp = scipy.interpolate.interp1d(shortened_t, shortened_data, kind='linear')
t_new = np.linspace(0, len(data) / sample_rate, num=len(data))
reconstructed_data_linear = linear_interp(t_new)

# 多项式拟合
degree = 5
coeffs = np.polyfit(shortened_t, shortened_data, degree)
poly = np.poly1d(coeffs)
reconstructed_data_poly = poly(t_new)

# 绘制结果
plt.figure(figsize=(12, 6))

plt.subplot(2, 1, 1)
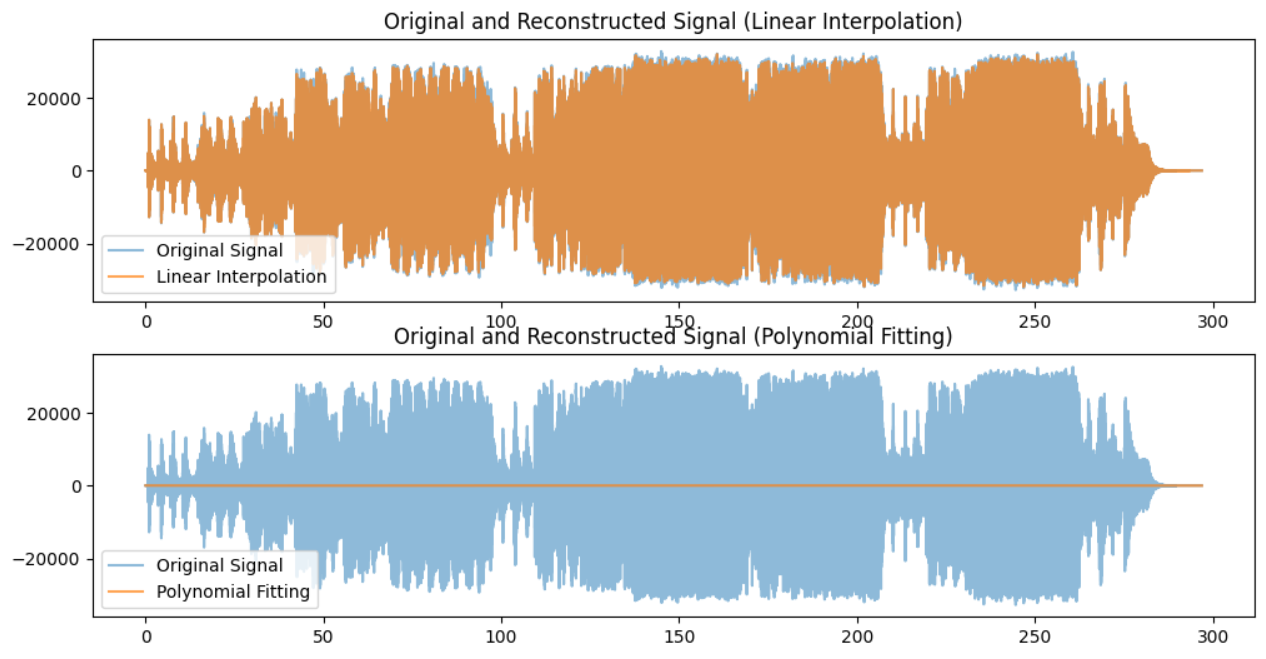
plt.title('Original and Reconstructed Signal (Linear Interpolation)')
plt.plot(t, data, label='Original Signal', alpha=0.5)
plt.plot(t_new, reconstructed_data_linear, label='Linear Interpolation', alpha=0.7)
plt.legend()

plt.subplot(2, 1, 2)
plt.title('Original and Reconstructed Signal (Polynomial Fitting)')
plt.plot(t, data, label='Original Signal', alpha=0.5)
plt.plot(t_new, reconstructed_data_poly, label='Polynomial Fitting', alpha=0.7)
plt.legend()

plt.show()

# 保存重建后的音频信号
wav.write('reconstructed_audio_linear.wav', sample_rate, reconstructed_data_linear.astype(np.int16))
wav.write('reconstructed_audio_poly.wav', sample_rate, reconstructed_data_poly.astype(np.int16))

output

请注意，在运行此代码前需要安装SciPy库，并准备一个名为 input_audio.wav 的音频文件。代码展示了如何对音频信号进行下采样、线性插值重建和多项式拟合重建，并绘制原始信号与重建信号的对比图。

Jianghu`s Blog. Power by Vuepress.
Copyright © 2024 Jianghu